Η έννοια της συνάρτησης ή απεικόνισης όπως ονομάζεται διαφορετικά, στα μαθηματικά εκφράζει τη διαισθητική ιδέα της ντετερμινιστικής εξάρτησης μιας ποσότητας από μια άλλη. Μια συνάρτηση είναι ο τρόπος ή κανόνας με τον οποίο αντιστοιχίζεται μία μοναδική τιμή της εξαρτημένης ποσότητας σε κάθε τιμή της ανεξάρτητης ποσότητας. Μεταξύ δύο συνόλων, συνάρτηση είναι ο κανόνας με τον οποίο σε κάθε στοιχείο του ενός συνόλου από τα δύο σύνολα αντιστοιχίζεται μοναδικό στοιχείο του άλλου συνόλου.
Αν Α και Β είναι δύο σύνολα, γράφουμε f : Α → Β για μια αντιστοίχιση από το Α στο Β. Το Α λέγεται σύνολο ορισμού και το Β σύνολο τιμών. Κάθε στοιχείο a του Α λέγεται όρισμα της f και κάθε στοιχείο b του Β στο οποίο αντιστοιχίζεται ένα τουλάχιστον όρισμα a λέγεται τιμή ή εικόνα της f στο a, και γράφουμε b = f(a). Σύμφωνα με τον παραπάνω ορισμό, για να είναι η f συνάρτηση, θα πρέπει
αν f(a) ≠ f(a') τότε a ≠ a'
δηλαδή δυο τιμές που είναι διαφορετικές να μην αντιστοιχούν παρά σε διαφορετικά ορίσματα. Λέμε τότε ότι η f είναι καλά ορισμένη (ενν. ως συνάρτηση).
Ο όρος απεικόνιση χρησιμοποιείται συνήθως γενικευτικά, στην περίπτωση που τα σύνολα Α και Β (ιδιαίτερα το Β), δεν είναι συνήθη σύνολα αριθμών.
Το γράφημα της συνάρτησης f : A → B είναι το σύνολο που αποτελείται από τα ζευγάρια της αντιστοίχισης
G(f) = {(a,b) ![]() A×B, όπου b = f(a)}
A×B, όπου b = f(a)}
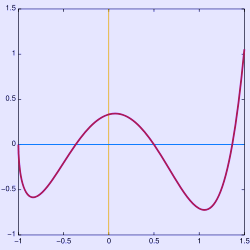
Γραφική παράσταση μιας συνάρτησης,
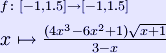
Η αντίστροφη αντιστοίχιση f-1 της συνάρτησης f είναι η αντιστοίχιση από το Β στο Α, που ορίζεται ως εξής:
f-1(b) = a ανν f(a) = b
Η αντίστροφη αντιστοίχιση μιας συνάρτησης δεν είναι πάντοτε συνάρτηση, μια και δεν υπακούει απαραίτητα στο αξίωμα μονοτιμίας: ένα στοιχείο b μπορεί να είναι τιμή δύο διαφορετικών ορισμάτων a και a' της f. Στην περίπτωση πάντως που είναι, η f λέγεται αντιστρέψιμη και η f-1 αντίστροφη συνάρτηση της f.
Ορισμοί
* Στα πλαίσια της θεωρίας συνόλων η συνάρτηση ορίζεται από το γράφημά της. Συγκεκριμένα, μια συνάρτηση f : A → B θεωρείται ως σχέση μεταξύ των Α και Β, δηλαδή ως ένα σύνολο f ![]() A×B, η οποία υπακούει στο αξίωμα της μονοτιμίας, που εδώ παίρνει την εξής μορφή:
A×B, η οποία υπακούει στο αξίωμα της μονοτιμίας, που εδώ παίρνει την εξής μορφή:
αν (a,b) ![]() f και (a,b')
f και (a,b') ![]() f τότε b = b'
f τότε b = b'
* Από την άποψη της μαθηματικής λογικής, η έννοια της συνάρτησης εκφράζεται με βάση μια τυπική γλώσσα ως ένα σύμβολο f βαθμού 2, το οποίο πάλι υπακούει στο αξίωμα μονοτιμίας:
αν f(a,b) και f(a,b') τότε b ≡ b'
* Στα πλαίσια του λαμδαλογισμού, η έννοια της συνάρτησης εκφράζεται με βάση μία τυπική γλώσσα ως λογικός όρος t, ο οποίος μπορεί αξιωματικά να
o εφαρμόζεται σε άλλον όρο s, ο οποίος συμπεριφέρεται ως όρισμα, με αποτέλεσμα έναν νέο όρο t(s)
o λαμδαποσπάται ως προς κάποια του μεταβλητή x, με αποτέλεσμα έναν νέο όρο λx.t, ο οποίος συμπεριφέρεται ως γενικός κανόνας αντιστοίχισης μέσα από τον κανόνα της αντικατάστασης:
(λx.t)(s) = t[x:=s]
Η συνηθισμένη διαισθητική ερμηνεία των παραπάνω είναι ότι "το x αντιστοιχίζεται στο t(x), ώστε αν εφαρμοστεί σε όρισμα s, τότε θα προκύψει η τιμή t(s)".
Είδη συναρτήσεων
* Μία συνάρτηση f : A → B λέγεται ένα προς ένα (1-1) ή αμφιμονότιμη ή αμφιμονοσήμαντη ή ένεση, όταν αντιστοιχίζει κάθε όρισμα σε αποκλειστικά δική του τιμή, δηλαδή όταν διαφορετικά ορίσματα απεικονίζονται σε διαφορετικές τιμές:
αν a ≠ a' τότε f(a) ≠ f(a')
* Μία συνάρτηση f : A → B λέγεται επί (με την έννοια: "το Α απεικονίζεται μέσω της f επί του Β, πάνω στο Β") ή έφεση, όταν δεν υπάρχει στοιχείο στο Β που να μην είναι η εικόνα κάποιου στοιχείου στο Α:
για κάθε b∈B υπάρχει a∈A ώστε b = f(a)
* Μία συνάρτηση ταυτόχρονα αμφιμονότιμη και επί λέγεται αμφίεση.
Από πολλούς μαθηματικούς, ο όρος "αμφιμονότιμη συνάρτηση" δεν χρησιμοποιείται ως συνώνυμο του "ένα προς ένα συνάρτηση" παρά ως συνώνυμο του "αμφίεση". Το δε επίθημα "-εση" (<ίημι) αποδίνει το γαλλικό "-jection" (<λατ. jacere), και έτσι τα "ένεση-έφεση-αμφίεση" αποδίνουν τα "injection-surjection-bijection" αντίστοιχα, τα οποία έχουν επικρατήσει στη δυτική μαθηματική νομενκλατούρα.
Σύγκριση συναρτήσεων και πράξεις
Μία συνάρτηση f είναι ίση με μία συνάρτηση g όταν έχουν το ίδιο σύνολο ορισμού, το ίδιο σύνολο τιμών και αντιστοιχίζουν ίσα ορίσματα σε ίσες τιμές:
f(a) = b ανν g(a) = b
Σύμφωνα εξάλλου με τη συνολοθεωρητική προσέγγιση, δύο συναρτήσεις είναι ίσες όταν τα γραφήματά τους ταυτίζονται (ως σύνολα).
* Η (ξένη) ένωση δύο συναρτήσεων f : A → B και g : A' → B', όπου τα Α, Α' είναι σύνολα ξένα μεταξύ τους, είναι η αντιστοίχιση f∪g: A∪A' → B∪B' που ορίζεται ως
f∪g(a) = f(a) και f∪g(a') = g(a')
για κάθε a∈A, a'∈A'.
* Η τομή δύο συναρτήσεων f : A → B και g : A' → B' είναι η αντιστοίχιση f∩g: A∩A' → B∩B' που ορίζεται ως
f∩g(a) = b ανν f(a)=g(a)=b
για κάθε a∈ A∩A'.
* Η σύνθεση της συνάρτησης f : A → B με την g : B → C είναι η αντιστοίχιση gof: A → C, που ορίζεται ως
gof(a) = g(f(a))
για κάθε a∈ A∩A'.
Ιδιότητες
* Μια συνάρτηση είναι αντιστρέψιμη αν και μόνο αν είναι αμφίεση.
* H ένωση δύο συναρτήσεων είναι πάλι συνάρτηση, ενώ η τομή όχι πάντα (ωστόσο είναι πάντα μερική συνάρτηση, δες παρακάτω).
* Η σύνθεση δύο συναρτήσεων είναι επίσης συνάρτηση.
* Αν f : A → B και g : B → C είναι ενέσεις τότε και η σύνθεσή τους gof είναι ένεση.
* Αν f : A → B και g : B → C είναι εφέσεις τότε και η σύνθεσή τους gof είναι έφεση.
Γενικεύσεις
* Μία αντιστοίχιση f : A → B, η οποία δεν είναι απαραίτητα μονότιμη, αλλά μπορεί να αποδίνει περισσότερες από μία τιμές σε ένα όρισμα, λέγεται πολύτιμη ή πλειότιμη ή πολυσήμαντη συνάρτηση. Παράδειγμα πολύτιμης συνάρτησης είναι η αντίστροφη αντιστοίχιση μιας συνάρτησης.
* Μία αντιστοίχιση f : A → B, η οποία δεν αποδίνει απαραίτητα τιμή σε κάθε όρισμα από το Α, λέγεται μερική συνάρτηση, και στην αντίθετη περίπτωση, ολική συνάρτηση. Στην περίπτωση της μερικής συνάρτησης, λέμε ότι η f ορίζεται σε κάποιο στοιχείο a του Α όταν το αντιστοιχίζει σε κάποιο στοιχείο b του Β· το υποσύνολο Α' του συνόλου ορισμού Α στο οποίο η f ορίζεται, λέγεται πεδίο ορισμού (ακόμη, πεδίο), και το υποσύνολο Β' του συνόλου τιμών Β, που αποτελείται από τις εικόνες της f, λέγεται πεδίο τιμών (ακόμη, συμπεδίο) της f.
* Μία αντιστοίχιση F : (A → B) → C, που δέχεται δηλαδή συναρτήσεις f : A → B ως ορίσματα και τους αποδίνει τιμή F(f) μέσα στο C, και ακόμη υπακούει στο αξίωμα της μονοτιμίας, λέγεται συναρτησιακό ή συναρτησοειδές. Τυπικά παραδείγματα συναρτησιακών στη μαθηματική ανάλυση είναι το ολοκλήρωμα και η παράγωγος συνάρτησης.
Δείτε ακόμη
* Γραφική παράσταση συνάρτησης
* Συνέχεια συνάρτησης
* Πραγματική συνάρτηση
* Μιγαδική συνάρτηση
* Συναρτησιακό και Τελεστής
* Μερική συνάρτηση
* Σχέση
* Συνάρτηση μεταφοράς
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
<@=@=@>
