Στα μαθηματικά πρώτος αριθμός (ή απλά πρώτος) είναι ένας φυσικός αριθμός μεγαλύτερος της μονάδας με την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του.
Το μηδέν και το ένα δεν είναι πρώτοι αριθμοί. (Το μηδέν συχνά δεν θεωρείται ούτε φυσικός).
Η ακολουθία των πρώτων ξεκινάει όπως παρακάτω
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113 ...
Ο αριθμός 2 είναι ο μόνος άρτιος πρώτος αριθμός. Όλοι οι άλλοι πρώτοι είναι περιττοί.
Αναπαριστώντας φυσικούς αριθμούς ως γινόμενα πρώτων παραγόντων
Το θεμελιώδες θεώρημα της αριθμητικής βεβαιώνει ότι κάθε θετικός ακέραιος γράφεται ως γινόμενο πρώτων παραγόντων με μοναδικό τρόπο. Για παράδειγμα:
Πλήθος πρώτων
Οι πρώτοι αριθμοί έχουν άπειρο πλήθος. Η πρόταση αυτή έχει αποδειχτεί με διάφορους τρόπους. Η πρώτη γνωστή απόδειξη είναι του Ευκλείδη:
Έστω ότι οι πρώτοι έχουν πεπερασμένο πλήθος n και είναι οι p1,p2,p3,...,pn. Ορίζουμε τον ακέραιο
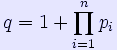
αυτός ο αριθμός δεν διαιρείται με κανένα πρώτο και αυτό είναι άτοπο ΟΕΔ.
Εύρεση πρώτων
Κόσκινο του Ερατοσθένη (*).
Η εύρεση των πρώτων αριθμών απασχόλησε από την αρχαιότητα τους μαθηματικούς. Ένας από τους πιο απλούς αλλά και αργούς τρόπους για (μαζική) εύρεση πολλών πρώτων είναι το λεγόμενο κόσκινο του Ερατοσθένη: Στο σύνολο των φυσικών αριθμών - πρακτικά έως κάποιο μεγάλο αριθμό Ν - αρχίζουμε και αποκλείουμε πρώτα τα πολλαπλάσια του 2 μετά τα πολλαπλάσια του επόμενου μη διαγραμμένου αριθμού κ.ο.κ. έως το Ν. Παρατηρούμε ότι όλο και λιγότερους αριθμούς θα βρίσκουμε προς διαγραφή. Οι αριθμοί που θα απομείνουν είναι όλοι πρώτοι. Το κόσκινο του Ερατοσθένη είναι ένας αργός αλγόριθμος για το άν ένας συγκεκριμένος αριθμός Ν είναι πρώτος ή όχι, διότι μεταξύ άλλων απαιτεί ουσιαστικά και την εύρεση όλων των πρώτων μικρότερων ίσων του 
(αν ένας αριθμός Ν δεν έχει διαιρέτες μικρότερους ίσους του τοτε έναι πρώτος).
Αλγόριθμοι για την πιστοποίηση πρώτων αριθμών
Παρατίθενται μερικοί αλγόριθμοι (κατά σειρά ταχύτητας ή και απλότητας) για την εύρεση άν ο Ν>=2 είναι πρώτος. Η σειρά επίσης αυτών των αλγορίθμων είναι παιδευτική για την εισαγωγή σε μια σειρά από προγράμματα για ηλεκτρονικούς υπολογιστές.
Απλός 1 - από τον ορισμό του πρώτου αριθμού
* Εξετάζουμε διαδοχικά όλους τους ακέραιους Μ<Ν
* Μόλις βρεθεί διαιρέτης του Ν σταματάμε και ο Ν δεν είναι πρώτος
* Αν εξαντληθούν οι Μ χωρίς να βρεθεί διαιρέτης, τότε ο Ν είναι πρώτος
Απλός 2
Βασιζόμενοι στην παρατήρηση ότι κανένας αριθμός Ν δεν έχει διαιρέτη μεγαλύτερο του Ν/2, τροποποιούμε τον παραπάνω αλγόριθμο εξετάζοντας όλους τους αριθμούς Μ<Ν/2.
Απλός 3
Παρατηρούμε ότι αν ένας αριθμός Ν δεν είναι πρώτος τότε έχει (τουλάχιστον) δύο διαιρέτες μεγαλύτερους από 1. Παρατηρούμε ότι σε αυτή την περίπτωση τουλάχιστον ένας διαιρέτης είναι μικρότερος από την τετραγωνική ρίζα του αριθμού. Τροποποιούμε τον παραπάνω αλγόριθμο εξετάζοντας όλους τους αριθμούς Μ < αν το δεν είναι ακέραιος. Αλλιώς ο αριθμός δεν είναι πρώτος αφού τον διαιρεί και η τετραγωνική του ρίζα.
Απλός 4
Με το πρόγραμμα Γλωσσομάθεια μπορεί να φτιαχτει αλγόριθμος ο οποίος ελέγχει αν ο εισαγόμενος αριθμός ειναι πρώτος ή όχι. Ο αλγόριθμος βασίσεται στο Θεώρημα του Ουίλσον. Ο αλγόριθμος ειναι ο παρακάτω.
ΠΡΟΓΡΑΜΜΑ Π
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ: Ν
ΑΡΧΗ
ΔΙΑΒΑΣΕ Ν
ΟΣΟ Ν<=100 ΕΠΑΝΑΛΑΒΕ
ΑΝ (Παραγοντικό(Ν-1) +1) MOD Ν =0 ΤΟΤΕ
ΓΡΑΨΕ 'Ο', Ν ,'ΕΙΝΑΙ ΠΡΩΤΟΣ'
ΑΛΛΙΩΣ_ΑΝ (Παραγοντικό(Ν-1) +1) MOD Ν <>0 ΤΟΤΕ
ΓΡΑΨΕ 'ΔΕΝ ΕΙΝΑΙ'
ΤΕΛΟΣ_ΑΝ
ΔΙΑΒΑΣΕ Ν
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
ΤΕΛΟΣ_ΠΡΟΓΡΑΜΜΑΤΟΣ Π
ΣΥΝΑΡΤΗΣΗ Παραγοντικό(αριθμός): ΑΚΕΡΑΙΑ
ΜΕΤΑΒΛΗΤΕΣ
ΑΚΕΡΑΙΕΣ: αριθμός, i, παρ
ΑΡΧΗ
παρ <-- 1
ΓΙΑ i ΑΠΟ 2 ΜΕΧΡΙ αριθμός
παρ <-- παρ*i
ΤΕΛΟΣ_ΕΠΑΝΑΛΗΨΗΣ
Παραγοντικό <-- παρ
ΤΕΛΟΣ_ΣΥΝΑΡΤΗΣΗΣ
Το πρόγραμμα φτιάχτηκε απο τον Βαγγελη Ρήγα .
Ο μεγαλύτερος γνωστός πρώτος αριθμός
Στις 4 Σεπτεμβρίου 2006 ανακαλύφθηκε ο μεγαλύτερος γνωστός πρώτος αριθμός. Είναι ο 232.582.657 − 1 και έχει 9.808.358 ψηφία. Έχει 650.000 περισσότερα ψηφία από τον προηγούμενο μεγαλύτερο πρώτο αριθμό, που είχε βρεθεί τον Δεκέμβριο του 2005. Τον ανακάλυψαν οι Κέρτις Κούπερ και Στίβεν Μπουν, καθηγητές του Κρατικού Πανεπιστημίου του Κεντρικού Μιζούρι, μέσω του προγράμματος GIMPS (Great Internet Mersenne Prime Search).
Ιδιότητες πρώτων
* Αν ο p είναι πρώτος και διαιρεί το γινόμενο ab γιά κάποιους ακέραιους a, b τότε ο p διαιρεί το a ή το b. (Ευκλείδης)
* Αν p πρώτος και a ακέραιος, τότε το ap − a διαιρείται από το p (Μικρό Θεώρημα του Φερμά).
* Ένας ακέραιος p > 1 είναι πρώτος αν και μόνο αν p - 1 παραγοντικό + 1 δηλ. το (p − 1)! + 1 διαιρείται από το p (Θεώρημα του Ουίλσον).
Ανοικτά ερωτήματα
Ένα από τα ανοιχτά ερωτήματα της σύγχρονης θεωρίας αριθμών είναι το πρόβλημα της παραγοντοποίησης μεγάλων ακεραίων, δηλαδή της εύρεσης αλγορίθμου παραγοντοποίησης σε πολυωνυμικό χρόνο. Στην "σκιά" αυτού του προβλήματος αναπτύχθηκε η κρυπτογραφία δημόσιου κλειδιού και ειδικότερα του κρυπτοσυστήματος RSA.
Oι εικασίες του Γκόλντμπαχ
Δείτε το κύριο άρθρο επί του θέματος: Εικασία του Γκόλντμπαχ
Είναι πολύ γνωστή η πρώτη εικασία που διατύπωσε ο Κρίστιαν Γκόλντμπαχ 1690-1764, η οποία σχετίζεται με τους πρώτους αριθμούς. Ο Γκόλντμπαχ υποστήριξε οτι κάθε άρτιος αριθμός μεγαλύτερος του 2, μπορεί να γραφεί σαν άθροισμα δύο πρώτων αριθμών. Η απόδειξη της παραπάνω εικασίας ταλανίζει ακόμα και σήμερα τους μαθηματικούς, καθώς παράλληλα οι υπολογιστές επιβεβαιώνουν την εικασία για όλο και μεγαλύτερους αριθμούς. το 1998, η εικασία επιβεβαιώθηκε για αριθμούς μέχρις και της τάξης του 1014
Η δεύτερη εικασία του Γκόλντμπαχ έγκειται στο ότι κάθε περιττός αριθμός μεγαλύτερος του 6 είναι άθροισμα τριών πρώτων αριθμών. Και αυτή η εικασία παραμένει αναπόδειχτη, αν και επιβεβαιώνεται από ηλεκτρονικούς υπολογιστές. Τυχόν απόδειξη της πρώτης εικασίας του Γκόλντμπαχ θα αποδείκνυε αμέσως και τη δεύτερη εικασία.
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
<@=@=@>
