HellenicaWorld

Η χρυσή τομή δηλώνει την αναλογία που ισούται περίπου με 1:1,618. Θεωρείται ότι δίνει αρμονικές αναλογίες και για το λόγο αυτό έχει χρησιμοποιηθεί στην αρχιτεκτονική και τη ζωγραφική, κατά την Αναγέννηση. Η χρυσή τομή ονομάστηκε προς τιμήν του Φειδία.

Μαθηματικός τύπος

Η χρυσή τομή δίνει το σημείο που πρέπει να διαιρεθεί ένα ευθύγραμμο τμήμα, ώστε ο λόγος του ως προς το μεγαλύτερο τμήμα να ισούται με τον λόγο του μεγαλύτερου τμήματος ως προς το μικρότερο.

Από το (2)=(3) έχουμε και αντικαθιστώντας στο (1)=(3) προκύπτει

Η εξίσωση αυτή έχει μόνο μία θετική ρίζα, την

Ιδιότητες

* Από την παραπάνω εξίσωση προκύπτει σύμφωνα με την οποία μπορούμε να εκφράσουμε το ως άπειρο διαδοχικό κλάσμα:

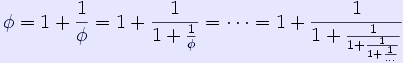
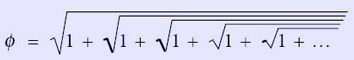
* Το αποτελεί το όριο του πηλίκου δύο διαδοχικών αριθμών Φιμπονάτσι.

Κατασκευή με κανόνα και διαβήτη

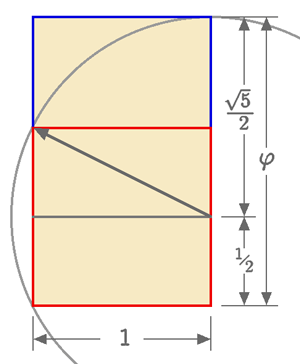
1. Κατασκευάζουμε τετράγωνο πλευράς 1 (κόκκινο).

2. Χωρίζουμε το τετράγωνο σε δύο ίσα ορθογώνια (πλευρών 1 και 1/2) και φέρνουμε μία διαγώνιο (γκρι).

3. Κατασκευάζουμε κύκλο με κέντρο το μέσο της μίας πλευράς του τετραγώνου και ακτίνα τη διαγώνιο του ορθογωνίου.

4. Προεκτείνουμε την πλευρα του τετραγώνου πάνω στην οποία βρίσκεται το κέντρο του κύκλου ως τον κύκλο (μπλε).

Το ευθύγραμμο τμήμα που αποτελείται από την πλευρά του τετραγώνου μαζί με την προέκταση εχει μήκος φ.

Η Χρυσή Αναλογία , εμφανίζεται στο πρόσωπο του πίνακα "Mona Lisa" του Leonardo Da Vinci.

δεν εμφανίζεται στην κατασκευή αρχαίων δομικών έργων όπως ο Παρθενώνας οπως μερικοί λένε!

Παρθενώνας: W = 30.88 m , L = 69.5 m και H = 13.72 m. για r = 9/4 περίπου ισχύει: r*H = W, r*W = L και r²*H = L

Ακολουθία Fibonacci

Μαθηματικά