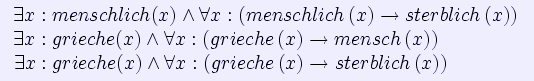|
|
Die Syllogismen (Mehrzahl von Syllogismus) bilden den Kern der klassischen Logik des Aristoteles in den Analytiken (Analytica Priora, Analytica Posteriora). Sie sind ein Katalog von Typen logischer Schlussfolgerungen. Diese Folgerungen sind immer nach dem gleichen Muster aufgebaut. Jeweils zwei Prämissen (Voraussetzungen), genannt Obersatz und Untersatz ergeben eine Konklusion (Schlussfolgerung). Innerhalb dieser drei kategorischen Urteile werden wiederum drei Begriffe verwendet, die der Syllogismus in Beziehung setzt: das Prädikat (P), das auf der rechten Seite der Konklusion und im Obersatz vorkommt, das Subjekt (S), das auf der linken Seite der Konklusion und im Untersatz vorkommt, und der Mittelbegriff (M), der im Obersatz und im Untersatz, nicht aber in der Konklusion vorkommt. Beispiel Prämisse 1 (oder Obersatz): Alle Menschen (M) sind sterblich (P). Der Syllogismus setzt also zwei zunächst nicht verbundene Begriffe (P und S) über den Mittelbegriff (M) in eine logisch gültige Beziehung, indem er von logisch gültigen Beziehungen jeweils eines Einzelbegriffes zum Mittelbegriff ausgeht. Geschichte Die syllogistische Logik ist aus dem Disputationsbetrieb der Platonischen Akademie hervorgegangen. Nach ersten Ansätzen in seiner "Topik" hat Aristoteles sie in den beiden "Analytiken" erstmals systematisch dargestellt. Allerdings kennt Aristoteles nur die ersten drei Figuren, die vierte wurde wahrscheinlich von Galen hinzugefügt. Michael Psellos hat wohl als erster den Gebrauch von Buchstabenbezeichnungen für Quantität und Qualität der Urteile benutzt sowie die Abkürzungsnamen für die Bezeichnung der einzelnen Schlüsse eingeführt; von ihm soll auch das "Logische Quadrat" stammen. Durch die Übersetzung seiner logischen Abhandlung wurden diese Bezeichnungen auch im lateinischen Mittelalter gebräuchlich. In der Scholastik erhielt die Syllogistik die Form, die dann Jahrhunderte lang in den Lehrbüchern tradiert wurde, wobei das Verständnis und die authentische Gestalt der Aristotelischen Syllogistik verloren ging und seit der Renaissance zunehmend scharfer Kritik unterzogen wurde (berühmt ist etwa die Kritik von René Descartes). Erst Jan Łukasiewicz hat Aristoteles' Logik in einer bahnbrechenden Arbeit neu entdeckt und sie vom Standpunkt der modernen Logik aus axiomatisch rekonstruiert; wegen der hohen Zahl der dabei angesetzten Axiome ist jedoch zu bezweifeln, ob diese Rekonstruktion wirklich gegenstandsadäquat ausgefallen ist. An Łukasiewicz schließt die neuere Forschung an, die ihr Standardwerk in Günther Patzigs Darstellung (1959) gefunden hat. Typen von Aussagen Eine Aussage in einem Syllogismus setzt immer zwei Begriffe in eine Beziehung (kategorisches Urteil). Dabei werden nur vier Typen von Urteilen bezüglich der Beziehung zwischen einem Subjekt (S) und einem Prädikat (P) betrachtet:
Die Vokale stammen dabei aus den lateinischen Worten "affirmo" (ich bejahe) und "nego" (ich verneine), wobei jeweils der erste Vokal für ein allgemeines, der zweite für ein partikuläres Urteil steht. Logisches Quadrat
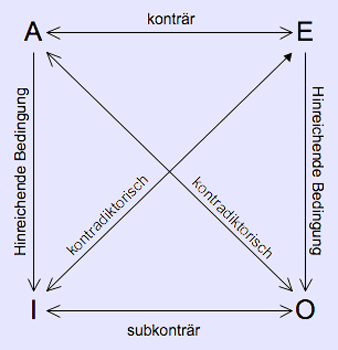
Das logische Quadrat Zwischen den unterschiedlichen Aussagentypen bestehen verschiedene Beziehungen: Zwei Aussagen bilden einen kontradiktorischen Gegensatz genau dann, wenn beide weder gleichzeitig wahr noch gleichzeitig falsch sein können, mit anderen Worten: Wenn beide unterschiedliche Wahrheitswerte haben müssen. Das wiederum ist genau dann der Fall, wenn die eine Aussage die Negation der anderen ist (und umgekehrt). Für die syllogistischen Aussagentypen trifft das kontradiktorische Verhältnis auf die Paare A-O und I-E zu. Zwei Aussagen bilden einen konträren Gegensatz genau dann, wenn sie zwar nicht beide zugleich wahr, wohl aber beide falsch sein können. In der Syllogistik steht nur das Aussagenpaar A–E in konträrem Gegensatz. Zwei Aussagen bilden einen subkonträren Gegensatz genau dann, wenn nicht beide zugleich falsch (wohl aber beide zugleich wahr) sein können. In der Syllogistik steht nur das Aussagenpaar I-O in subkonträrem Gegensatz. In der Syllogistik wird das allgemein bejahende Urteil so verstanden, dass das Subjekt S nicht leer ist. Die Aussage "Alle S sind P" setzt also voraus bzw. sagt mit aus, dass es überhaupt S gibt. Unter dieser Voraussetzung besteht zwischen den Aussagetypen A und I einerseits und E und O andererseits ein Folgerungszusammenhang: Aus A folgt I, d.h. wenn alle S P sind, dann gibt es auch tatsächlich S, die P sind; und aus E folgt O, d.h. wenn keine S P sind, dann gibt es tatsächlich S, die nicht P sind. Diese Zusammenhänge werden oft in einer Tabelle, die unter dem Namen "Logisches Quadrat" bekannt wurde, zusammengefasst (siehe Abbildung). Existenzielle Voraussagen Wie schon im logischen Quadrat ersichtlich, macht die Syllogistik bei allgemeinen Urteilen Existenzaussagen über das Subjekt, d.h. sie setzt voraus, dass das Subjekt nicht leer ist: Die Aussage "Alle S sind P" sagt mit aus, dass es tatsächlich S gibt, meint also: "Es gibt S, und alle davon sind P". Die Aussage "Keine S sind P" sagt mit aus, dass es tatsächlich S gibt, meint also: "Es gibt S, und keine davon sind P". Obwohl diese existenziellen Voraussetzungen dem natürlichen Sprachgebrauch entsprechen (normalerweise empfindet man nur Allaussagen über tatsächlich vorhandene Dinge als sinnvoll), ist es wichtig, sich ihrer bewusst zu sein, weil es durchaus auch logische Systeme gibt, die diese Voraussetzungen nicht machen. Figuren Welche der drei Begriffe S, P und M in einer Aussage des Syllogismus vorkommen müssen, ist festgelegt: Der Obersatz besteht aus P und M, der Untersatz aus S und M, die Konklusion aus S und P. Die Konklusion hat dabei immer die Form S - P, die Anordnung der Begriffe in den Prämissen kann frei gewählt werden. Je nach Anordnung unterscheidet man die vier Figuren:
Beispiel Prämisse 1 (oder Obersatz): Alle Menschen (M) sind sterblich (P). Aufgrund der Stellung der Begriffe M - P, S - M, S - P erkennt man einen Syllogismus der 1. Figur. Modi (Kombinationen) Es gibt in jeder Figur mehrere Modi (auch: Kombinationen), die sich voneinander durch die Typen der auftretenden Urteile unterscheiden. Jede der drei Aussagen im Syllogismus kann von einem der vier Typen A, E, O, I sein. Bei vier Figuren, vier Typen und drei Aussagen ergeben sich also 256 Kombinationsmöglichkeiten also theoretische Syllogismen. Die meisten von diesen (nämlich 232) ergeben allerdings keinen gültigen Schluss. Ein Modus wird durch drei Buchstaben beschrieben. Dabei stehen die ersten beiden Buchstaben für die Typen der Prämissen, der dritte Buchstabe für den Typ der Konklusion.
Beispiel Prämisse 1 (oder Obersatz): Alle Menschen (M) sind sterblich (P). Alle drei Aussagen sind vom Typ A, also ist das ein AAA-Syllogismus. Mit Hilfe der Regeln des einfachen kategorischen Syllogismus erkennt man 24 Typen von korrekten Schlüssen, die folgende Namen tragen:
Dabei bezeichnen die Vokale die Typen der Aussagen in der Reihenfolge Obersatz, Untersatz, Konklusion. Die Konsonanten geben an, aus welchem der Syllogismus der 1. Figur (1. Buchstabe) und durch welche Veränderung (jeweils auf Vokal folgender Konsonant) die Syllogismen der anderen Figuren hergeleitet werden können. Die 15 fett gedruckten Modi sind uneingeschränkt gültig, die übrigen 9 haben sog. „starke“ Prämissen aber „schwache“ Konklusionen, da ihre partikularen Urteile bereits in den allgemeinen Urteilen der starken Konklusionen enthalten sind. Beispiele: Modus Barbara (stark): Alle Münchner sind Bayern, alle Schwabinger sind Münchner, es folgt: Alle Schwabinger sind Bayern. Modus Barbari (schwach): Alle Münchner sind Bayern, alle Schwabinger sind Münchner, es folgt: Einige Schwabinger sind Bayern. Modus Celarent (stark): Kein Münchner ist Passauer, alle Schwabinger sind Münchner, es folgt: Kein Schwabinger ist Passauer. Modus Celaront (schwach): Kein Münchner ist Passauer, alle Schwabinger sind Münchner, es folgt: Einige Schwabinger sind keine Passauer. Die schwachen Schlussfolgerungen sind dennoch logisch gültig, sofern gewisse Zusatzbedinungen erfüllt sind: Jeweils bestimmte Begriffe (Subjekt, Prädikat oder Mittelbegriff) dürfen nicht leer sein. Syllogismen im Kontext der modernen Mathematik
<@=@=@>
Die klassischen Syllogismen lassen sich heute als Anwendung der umfassenderen Prädikatenlogik verstehen. Auch lassen sie sich als Mengenbeziehungen darstellen. Beispiel Syllogismus: Alle Menschen sind sterblich. mengenmäßig: Menschen ist eine Untermenge von Sterbliche. prädikatenlogisch:
Metathesis praemissarum metathesis praemissarum (lat.) bezeichnet eine logische Operation im Syllogismus. Durch diese Operation werden die Prämisse minor und die Prämisse major miteinander vertauscht. Einfache Regeln für die Gültigkeit von Schlüssen 1. Ex mere negativis nihil sequitur (lat. Allein aus verneinten Aussagen können keine Schlüsse gezogen werden): bezeichnet eine Logikregel, nach der ein einfacher kategorischer Syllogismus nicht nur verneinende Prämissen enthalten darf. Aus den Prämissen "Kein Planet leuchtet selbst" und "Die Sonne ist kein Planet" kann z.B. kein wahrer Schlusssatz gewonnen werden. 2. Nihil sequitur geminis ex particularibus unquam (lat. Aus zwei partikularen Prämissen kann nichts gefolgert werden). Aus den Prämissen "Einige Säugetiere leben im Wasser" und "Einige Tiere, die auf dem Land leben, sind Säugetiere" kann ebenfalls kein wahrer Schlusssatz im Syllogismus abgeleitet werden. 3. Ambae affirmantes nequeunt generare negantem (lat. Aus zwei affirmativen Prämissen kann kein negativer Schlusssatz gefolgert werden.) Beispiele und Anmerkungen Zur ersten Figur des kategorischen Syllogismus Der Schluss der ersten Figur hat die Form MxP und SyM => SzP. Die erste Figur besitzt folgende vier Modi (auch: Kombinationen) mit den Namen: AAA - Modus Barbara Beispiel Alle Rechtecke sind Vierecke EAE - Modus Celarent Beispiel Kein Rechteck ist ein Kreis AII - Modus Darii Beispiel Alle Quadrate sind Rechtecke EIO - Modus Ferio Beispiel Kein Säugetier atmet durch Kiemen Zur zweiten Figur des kategorischen Syllogismus Der Schluss der zweiten Figur hat die Form # 2. Figur: PxM und SyM => SzP. Die zweite Figur besitzt folgende vier Modi (auch: Kombinationen) mit den Namen: EAE - Modus Cesare Beispiel Kein Säugetier atmet durch Kiemen AEE - Modus Camestres Beispiel Alle Fische atmen durch Kiemen EIO - Modus Festino Beispiel Kein Abgeordneter ist ein Gauner. AOO - Modus Baroco Beispiel Alle Professoren sind ernst. Zur dritten Figur des kategorischen Syllogismus Der Schluss der dritten Figur hat die Form MxP und MyS => SzP. Die dritte Figur besitzt folgende sechs Modi (auch: Kombinationen) mit den Namen: AAI - Modus Darapti Beispiel Alle Quadrate sind Vierecke Anmerkung Der Modus Darapti setzt voraus, dass das Subjekt nicht leer ist, dass es im Beispiel also tatsächlich Quadrate gibt; vergleiche Abschnitt Existenzielle Voraussagen. IAI - Modus Disamis Beispiel Einige Früchte sind Äpfel. AII - Modus Datisi Beispiel Alle Rechtecke sind Vierecke. EAO - Modus Felapton Beispiel Keine Münchner sind Passauer OAO - Modus Bocardo Beispiel Einige Münchner sind nicht Politiker EIO - Modus Ferison Beispiel Keine Münchner sind Passauer Zur vierten Figur des kategorischen Syllogismus Der Schluss der vierten Figur hat die Form PxM und MyS → SzP. Die vierte Figur besitzt folgende fünf Modi (auch: Kombinationen) mit den Namen: Die vierte Figur besitzt folgende fünf Modi (auch: Kombinationen) mit den Namen: AAI - Modus Bamalip Beispiel Alle Quadrate sind Rechtecke Anmerkung Der Modus Bamalip setzt voraus, dass das Subjekt nicht leer ist, dass es im Beispiel also tatsächlich Quadrate und Rechtecke gibt (wobei die Existenz letzterer in diesem Fall aus der Existenz ersterer bereits folgt); vergleiche Abschnitt Existenzielle Voraussagen AEE - Modus Camenes Beispiel Alle Passauer sind Bayern IAI - Modus Dimaris Beispiel Einige Rhomben sind Rechtecke EAO - Modus Fesapo Beispiel Keine Passauer sind Münchner Anmerkung Der Modus Fesapo setzt voraus, dass der Mittlebegriff nicht leer ist, dass es im Beispiel also tatsächlich Münchner gibt; vergleiche Abschnitt Existenzielle Voraussagen. EIO - Modus Fresion Beispiel Keine Passauer sind Münchner Syllogismen
<@=@=@>
Literatur
Weblinks
Von "http://de.wikipedia.org/"

|
||||||||||||||||||