Τελεστής ανάδελτα (Del operator), ή

Αν f , g είναι βαθμωτές συναρτήσεις των ανεξάρτητων μεταβλητών x, y, z τότε καλούμε Κλίση (gradf) του f:

Αν v είναι διανυσματική συνάρτηση των ανεξάρτητων μεταβλητών x, y, z τότε καλούμε divv Απόκλιση του v

Αν v είναι διανυσματική συνάρτηση των ανεξάρτητων μεταβλητών x, y, z τότε καλούμε curlv ( ή rotv) Περιστροφή του v

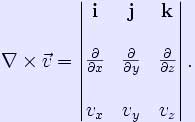
Αν u είναι διανυσματική συνάρτηση των ανεξάρτητων μεταβλητών x, y, z τότε

Ο τελεστής του Laplace Δ ορίζεται με

Πράξεις , Ιδιότητες

Αν A είναι διανυσματική συνάρτηση και f, g είναι βαθμωτές συναρτήσεις των ανεξάρτητων μεταβλητών x, y, z τότε:

, η περιστροφή της κλίσεως του f είναι μηδέν.

, η απόκλιση της περιστροφής του Α είναι μηδέν.

Κυλινδρικές συντεταγμένες

Μαθηματικά

Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License