Η συνάρτηση 'Οιλερ (Euler - από τον μαθηματικό Λέοναρντ Όιλερ Leonhard Euler) , η οποία έχει καθιερωθεί να συμβολίζεται με το ελληνικό γράμμα φ, είναι μια αριθμοθεωρητική συνάρτηση η οποία ορίζεται στους θετικούς ακέραιους αριθμούς.
Για κάθε θετικό ακέραιο 
, το 
μας δίνει το πλήθος των φυσικών αριθμών οι οποίοι είναι μικρότεροι ή ίσοι με το και οι οποίοι είναι πρώτοι με το (έχουν δηλαδή μέγιστο κοινό διαιρέτη τη μονάδα).
Για παράδειγμα ας θεωρήσουμε τον αριθμό 6. To 
είναι ίσο με 2, αφού από τους φυσικούς αριθμούς από το 1 μέχρι το 6 ακριβώς δύο, οι 1 και 5, είναι πρώτοι με το 6.
Η συνάρτηση του Όιλερ είναι πολύ χρήσιμη στην θεωρία αριθμών. Αρκεί και μόνο να παρατηρήσει κάποιος ότι το πλήθος των στοιχείων της πολλαπλασιαστικής ομάδας των ακεραίων modulo n είναι ακριβώς . Αυτό το γεγονός, μαζί με το θεώρημα του Λαγκράνζ, μας δίνουν την απόδειξη για το θεώρημα του Όιλερ που αποτελεί γενίκευση του μικρού θεωρήματος του Φερμά.
Ιδιότητες
Η συνάρτηση του Όιλερ είναι πολλαπλασιαστική συνάρτηση που σημαίνει ότι για δύο φυσικούς m,n με μκδ(m, n) =1 ισχύει 
.
Είναι εύκολο να παρατηρήσει κάποιος ότι αν ο n είναι πρώτος αριθμός τότε όλοι οι φυσικοί που είναι μικρότεροι από αυτόν είναι πρώτοι με το n, οπότε 
.
Με χρήση των παραπάνω και του Κινέζικου Θεωρήματος Υπολοίπων η τιμή της φ(n) μπορεί να υπολογιστεί με χρήση του Θεμελιώδους Θεωρήματος της Αριθμητικής:
Αν 
, όπου τα 
είναι διακεκριμένοι πρώτοι αριθμοί, τότε
Ο τελευταίος τύπος μπορεί να γραφτεί και ως εξής:
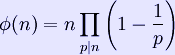
όπου το γινόμενο διατρέχει όλα τα pr.
Παραδείγματα
επειδή το 101 είναι πρώτος
Παρατηρήσεις
Μπορούμε να χρησιμοποιήσουμε επίσης την συνάρτηση αντιστροφής του Μέμπιους για να "αντιστρέψουμε" το γινόμενο σε άθροισμα και να πάρουμε έναν άλλο τύπο για την φ(n):
όπου με μ συμβολίζουμε την συνάρτηση του Μέμπιους πάνω από τους φυσικούς αριθμούς.
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License
<@=@=@>
