Η ζήτα συνάρτηση ή ζήτα συνάρτηση Riemann, από το όνομα του μαθηματικού Μπέρναρντ Ρίμαν είναι μια συνάρτηση με ιδιαίτερη σημασία στη θεωρία αριθμών, λόγω της σχέσης της με την κατανομή των πρώτων αριθμών. Έχει επίσης εφαρμογές σε άλλα πεδία, όπως η φυσική, η θεωρία πιθανοτήτων και η εφαρμοσμένη στατιστική.
Ορισμός
Η ζήτα συνάρτηση ορίζεται για κάθε μιγαδικό αριθμό με πραγματικό μέρος > 1 από τη σειρά Ντιρισλέ (Dirichlet):
Στην περιοχή 
, αυτή η σειρά συγκλίνει και ορίζει μια συνάρτηση αναλυτική σε αυτή την περιοχή.
Η ζήτα συνάρτηση συνδέεται με τους πρώτους αριθμούς με την εξής σχέση (γινόμενο του Ευκλείδη):
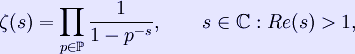
όπου 
το σύνολο όλων των πρώτων αριθμών.
Επεκτάσεις
Η ζήτα συνάρτηση μπορεί να επεκταθεί αναλυτικά στην περιοχή 
σε μία μερομορφική συνάρτηση στην περιοχή αυτή με έναν πόλο τάξής 1 στο s = 1. Η επεκταμένη αυτή συνάρτηση έιναι:
όπου 
( με 
δηλώνεται το ακέραιο μέρος του 
).
Η ζήτα συνάρτηση μπορεί να επεκταθεί αναλυτικά σε όλο το 
σε μία μερομορφική συνάρτηση στην περιοχή αυτή με έναν πόλο τάξής 1 στο s = 1. Για Re(s) > 1 − 2r η επεκταμένη αυτή συνάρτηση έιναι:
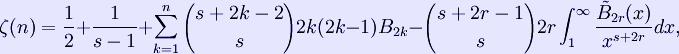
όπου B2k αριθμός Bernoulli και 
πολυώνυμο Bernoulli.
Σχέσεις
Συναρτηρησιακή εξίσωση της ζήτα συνάρτησης (functional equation):
όπου 
η γάμμα συνάρτηση.
H γάμμα συνάρτηση (ή ακριβέστερα η αναλυτική προέκτασή της στο έχει πόλους τάξής 1 στο 
. Η ζήτα συνάρτηση μηδενίζεται συνεπώς για 
.
Υπόθεση του Riemann
Η υπόθεση του Riemann είναι ένα από τα άλυτα προβλήματα της θεωρίας αριθμών. Δηλώνει ότι εκτός από τις τιμές η ζήτα συνάρτηση μηδενίζεται μόνο για 
με 
.
Από την συναρτηρησιακή εξίσωση της ζήτα συνάρτησης και τις ιδιότητες της γάμα συνάρτησης προκύπτει ότι η ζήτα συνάρτηση για 
με 
μηδενίζεται μόνο για . Στην περιοχή 
προφανώς δε μηδενίζεται. Επίσης αποδυκνείεται ότι 
για 
. Συνεπώς οι υπόλοιπες τιμές που τη μηδενίζουν πρέπει να ικανοποιούν 
.
Η υπόθεση του Riemann αποτελεί ένα από τα προβλήματα του ενός εκατομμυρίου δολαρίων.
Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License