Στα μαθηματικά, δευτεροβάθμια εξίσωση ονομάζεται κάθε πολυωνυμική εξίσωση δευτέρου βαθμού. Η γενική μορφή μιας δευτεροβάθμιας εξίσωσης είναι:

όπου τα γράμματα α, β και γ παριστάνουν σταθερούς αριθμούς, με

Οι σταθερές α, β και γ ονομάζονται συντελεστές, με το α να είναι ο συντελεστής του x², το β να είναι ο συντελεστής του x και γ ο σταθερός όρος. Οι συντελεστές μπορεί να είναι πραγματικοί ή μιγαδικοί αριθμοί.

Λύσεις δευτεροβάθμιας εξίσωσης

Κάθε δευτεροβάθμια εξίσωση έχει δύο λύσεις (ή διαφορετικά ρίζες) στο πεδίο των μιγαδικών αριθμών που μπορεί να είναι είτε διαφορετικές είτε ίσες (οι δύο λύσεις συμβολίζονται εδώ με και ). Οι λύσεις μιας δευτεροβάθμιας εξίσωσης μπορούν να βρεθούν με τον τύπο:

Διακρίνουσα

Η παράσταση Δ = β² − 4αγ ονομάζεται διακρίνουσα (σύμβολο Δ) της εξίσωσης και λέγεται έτσι γιατί χρησιμοποιείται για να διακρίνουμε τρεις ποιοτικά διαφορετικές περιπτώσεις λύσεων τις εξίσωσης. Όταν οι συντελεστές α,β και γ είναι όλοι πραγματικοί αριθμοί, διακρίνουμε τις πιο κάτω περιπτώσεις:

* Η διακρίνουσα είναι θετική.

Η εξίσωση έχει δύο λύσεις διαφορετικές και οι δύο πραγματικές. Γεωμετρικά αυτά σημαίνει ότι η παραβολή που αντιστοιχεί στην εξίσωση τέμνει τον άξονα των x σε δύο σημεία. Επιπλέον, αν οι συντελεστές είναι ακέραιοι και η διακρίνουσα εκτός από θετική είναι και τέλειο τετράγωνο, οι λύσεις της εξίσωσης είναι και οι δύο ρητοί αριθμοί και η εξίσωση μπορεί να αναλυθεί σε γινόμενο δύο παραγόντων. Οι δύο πραγματικες λύσεις είναι οι:

, και

* Η διακρίνουσα είναι ίση με μηδέν.

Η εξίσωση έχει μια διπλή ρίζα που είναι επιπλέον και πραγματική. Γεωμετρικά αυτό σημαίνει ότι η παραβολή αγγίζει (καλύτερα εφάπτεται) τον άξονα των x σε ένα σημείο. Αυτό συμβαίνει γιατί αν η διακρίνουσα είναι μηδέν η τετραγωνική ριζα που έχει μπροστά της το +/- εξαφανίζεται και παραμένει έτσι μία μόνο λύση, η οποία είναι η:

Μια δευτεροβάθμια εξίσωση με διακρίνουσα μηδέν μπορεί να παραγοντοποιηθεί σε τέλειο τετράγωνο.

* Η διακρίνουσα είναι αρνητική.

Η εξίσωση δεν έχει λύση στο σύνολο των πραγματικών αριθμών .

Ωστόσο, έχει δύο διαφορετικές λύσεις που είναι και οι δύο μιγαδικοί αριθμοί. Επιπλέον οι δύο λύσεις είναι μεταξύ τους συζυγείς μιγαδικές. Γεωμετρικά αυτό σημαίνει ότι η παραβολή ούτε τέμνει ούτε εφάπτεται του άξονα των x, για την ακρίβεια δεν έχει κανένα κοινό σημείο με αυτόν. Αν βγάλουμε ως κοινό παράγοντα από την τετραγωνική ρίζα το τότε οι δύο συζυγείς λύσεις είναι οι:

, και

Μια δευτεροβάθμια εξίσωση με διακρίνουσα αρνητική δεν μπορεί να παραγοντοποιηθεί.

Απόδειξη

Θέλουμε να φέρουμε την εξίσωση στη μορφή (ax + b)² = c ώστε να είναι πιο εύκολο να λυθεί. Aρχικά εξετάζουμε τους όρους με x² και x και τους χωρίζουμε από τη σταθερά γ: \

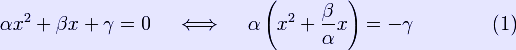
Κατόπιν προσθαφερούμε στο αριστερό μέλος της εξίσωσης κατάλληλη σταθερά, ώστε να σχηματιστει τετράγωνο:

και φέρνουμε τη σταθερά στο δεξί μέρος

Φερνουμε στο αριστερό μέρος όλα τα μεγέθη που μπορούν να γραφούν ως τετράγωνο

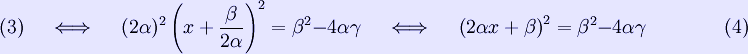
Το δεξί μέρος της εξίσωσης ονομάζεται διακρίνουσα Δ = β2 − 4αγ. Οπότε εχουμε φέρει την εξίσωση στη μορφή που θέλουμε και συγκεκριμένα:

Επειδή κάθε πραγματικός αριθμος υψωμένος στο τετράγωνο είναι μη αρνητικός (αριστερό μέρος της εξίσωσης), η διακρίνουσα (δεξί μέρος της εξίσωσης) πρέπει να είναι και αυτή μη αρνητικός αριθμός, , για να έχει η εξίσωση λύση στους πραγματικούς. Σε αυτή την περίπτωση ισχύει:

.

Οι τύποι του Vièta

Οι τύποι του Vièta δίνουν απλές σχέσεις μεταξύ των ριζών ενός πολυωνύμου και των συντελεστών του. Στην περίπτωση των δευτεροβάθμιων εξισώσεων παίρνουν την ακόλουθη μορφή:

, και

Αν συμβολίσουμε με S το άθροισμα των ριζών μιας δευτεροβάθμιας εξίσωσης και με P το γινόμενό τους τότε κάθε δευτεροβάθμια εξίσωση γράφεται και ώς εξής:

όπου

, και

Μαθηματικά

Από τη ελληνική Βικιπαίδεια http://el.wikipedia.org . Όλα τα κείμενα είναι διαθέσιμα υπό την GNU Free Documentation License

<@=@=@>