Satz von Menelaos

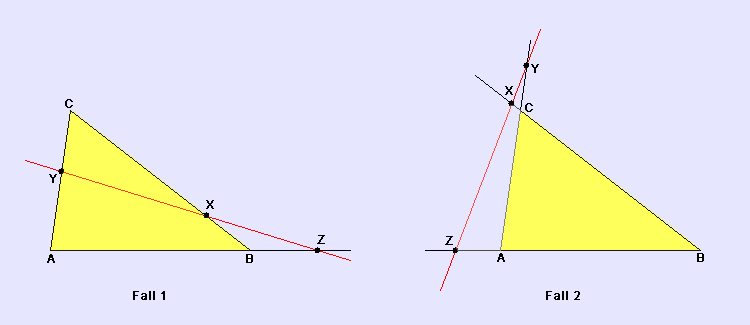
Der Satz von Menelaos, benannt nach dem griechischen Mathematiker Menelaos (Alexandria, etwa 100 n.Chr.), macht eine Aussage über Geraden, die Dreiecke schneiden.

Gegeben seien ein Dreieck ABC und eine Gerade, welche die Dreiecksseiten [BC], [CA] und [AB] beziehungsweise ihre Verlängerungen in den Punkten X, Y und Z schneidet. Dann gilt:

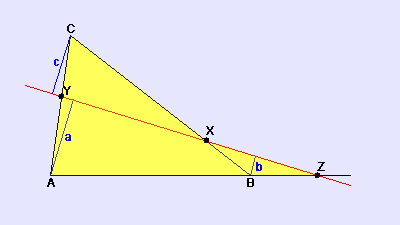
Umgekehrt kann man aus der Richtigkeit dieser Beziehung folgern, dass die Punkte X, Y und Z auf einer Geraden liegen.

Der Satz von Menelaos lässt sich mit Hilfe des Strahlensatzes beweisen. Man betrachtet drei Lote auf die gegebene Gerade, die von den Ecken A, B und C ausgehen. Die Längen der Lotstrecken seien mit a, b und c bezeichnet.

Aus dem Strahlensatz erhält man folgende Verhältnisgleichungen:

Multipliziert man diese drei Gleichungen miteinander, so ergibt sich

und weiter (durch Multiplikation mit dem Nenner)

.

Weblinks

• Menelaos' Theorem ein animierter, geometrischer Beweis des Satzes von Menelaos (englisch)